(서울=연합뉴스) 김준억 기자 = 신종 코로나바이러스 감염증(코로나19) 팬데믹이 언제 끝날지 예측하는 데 가장 중요한 수치는 'R값(감염재생산지수)'이다. 사회적 거리두기로 감염의 기회를 줄이면 R값은 낮아지고 확진자 수는 감소한다.

R값의 뿌리에는 영국의 열대병학자인 로널드 로스(1857∼1932)가 있다. 그는 수학 모형을 이용한 말라리아 연구로 1902년 노벨의학상을 받았고, 전염의 수학적 모델링을 확립한 '감염학의 아버지'라 할 수 있다.

그러나 1975년 유럽에서 말라리아가 종식될 때까지 감염병에서 R값을 낮추려는 노력은 외면당했다. 로스는 이를 한탄하며 "세상이 새로운 아이디어를 이해하는 데는 적어도 10년이 필요하다. 그게 아무리 중요하거나 간단해도 말이다"라는 말을 남겼다.

수학자이자 역학자인 애덤 쿠차르스키 런던 위생 열대의학 대학원 교수가 쓴 '수학자가 알려주는 전염의 원리'(원제 : RULES OF CONTAGION)는 바이러스와 금융위기, 가짜뉴스 등이 어떻게 퍼져나가고 멈추는지를 수학으로 설명한다.

이 책의 1장은 로스의 감염 모형을 기본으로 대규모로 발생한 감염병의 추이를 알려준다. 로스는 모기를 모두 없애지 않아도 말라리아를 관리할 수 있다는 계산 결과를 내놨다.

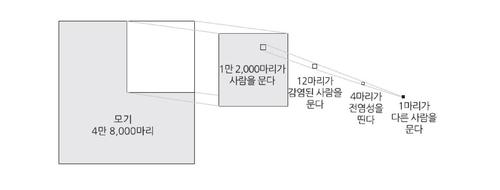
그는 1천명이 사는 마을에 감염된 사람이 1명 있는 시나리오로 설명했다. 전염되려면 모기 한 마리가 감염된 사람을 물어야 한다. 로스는 모기 4마리 중 1마리만 사람을 물 수 있다고 봤다. 따라서 어떤 지역에 모기 4만8천마리가 있다면 1만2천마리만 사람을 물 수 있다. 감염자는 1천명 중 1명이므로 모기 1만2천마리 중 12마리만 감염자를 물어 말라리아 기생충을 빨아들일 수 있다. 또 말라리아 기생충이 모기 안에서 번식하려면 시간이 걸리는 데 모기 3마리 중 1마리만 그 정도로 살 수 있다고 가정해 기생충을 빨아들인 12마리 중 4마리만 감염성을 띤다고 봤다. 4마리 중 1마리만 사람을 물기 때문에 모기가 4만8천마리가 있어도 새로운 감염자는 1명밖에 늘어나지 않는다는 것이다.



여기에 회복으로 감염을 상쇄되는 과정, 모기 밀도의 임계치 등을 더해 마지막 남은 모기까지 없애지 않아도 말라리아를 관리할 수 있다는 '모기 정리' 분석은 1910년 펴낸 '말라리아 예방'에 실렸다.

저자는 이런 감염의 원리는 바이러스 외에도 금융위기, 총기 폭력, 가짜뉴스, 랜섬웨어, 인터넷 유행 등에서도 적용된다고 말한다.

책은 미국 시카고시가 연쇄 총기 폭력을 해결하는 데 천연두 퇴치 메커니즘을 쓴 사례를 소개한다.

감염병 모델이 적용된 이유는 연쇄 폭력도 노출된 이후 증상이 나타날 때까지 시간 지연이 있다는 점이다. 잠복기 외에도 지도를 보면서 폭력의 동선을 파악할 때 익숙한 패턴이 보이기 때문이기도 하다.

천연두는 사람 간 감염에 시간이 오래 걸려 백신을 접종할 시간이 충분해 역학자들은 '포위 접종'이란 방법을 썼다. 새로운 감염 사례가 나타나면 감염자가 접촉했을 가능성이 있는 사람들을 찾아내 모두 접종하는 방식이다. 시카고시는 '폭력 구제'라는 집단을 이용해 사건 초반에 용의자 주위의 인물들을 관리하는 '포위 접종' 방식을 차용했다는 것이다.

책은 가짜뉴스도 전염의 원리로 살펴본다. 매사추세츠공대(MIT) 연구 결과 가짜뉴스가 진짜 뉴스보다 더 널리, 더 빨리 퍼지는 경향이 있는데, 가짜뉴스를 퍼뜨리는 사람은 보통 팔로워가 적은 이들이었다. 전염의 원리로 생각한다면 이는 전파 기회가 더 많다기보다는 전파 확률이 높기 때문이라고 설명한다.

저자는 SNS에서의 전염을 추적하는 이유는 해로운 정보를 드러내고 줄이는, 이른바 예방접종의 일환이라며 "해로운 콘텐츠와 맞서 싸우면 어떤 사람이 그 콘텐츠를 보지 못하도록 하는 직접적 효과와 동시에 다른 사람에게 퍼뜨리지 못하도록 하는 간접적 효과를 얻을 수 있다. R값에 조금만 손을 대도 아웃브레이크 규모를 크게 줄일 수 있다"고 말한다.

세종. 380쪽. 1만9천원.




justdust@yna.co.kr



<저작권자(c) 연합뉴스, 무단 전재-재배포 금지>